The Quadrilaterals part 1

Quadrilateral is a plane figure (polygon) with four sides and four vertices. It is also called tetragon and quadrangle. While in triangle, the sum of the interior angles is 180° ; for the quadrilaterals the sum of the interior angles is always equal to 360°

A + B + C + D = 360°

Classifications of Quadrilaterals

• Simple - sides of simple quadrilaterals do not cross each other
• Complex- sides of complex quadrilaterals cross each other

Classifications of Simple Quadrilaterals

• Convex- none of the sides pass through the quadrilateral when prolonged or extended
• Concave- prolongation of any one side will pass inside the quadrilateral

I. General Quadrilaterals

Note: This formulas are are applicable only to convex quadrilaterals.

Finding the Area of General Quadrilaterals given the four sides and sum of two opposite angles.

II. Cyclic Quadrilaterals

Acyclic quadrilateral is a quadrilateral in which all of its four vertices lie of a circle.

Finding the Area of Cyclic Quadrilaterals using Ptolemy's Theorem and Bramaguptha's Formula.

Ptolemy's Theorem

d₁ • d₂ = ac + bd

Note:

Opposite angles of cyclic quadrilateral are supplementary

A + C = 180°

B + D = 180°

III. Quadrilateral Circumscribing a Circle

Quadrilateral circumscribing a circle (also called tangential quadrilateral) is a quadrangle whose sides are tangent to a circle inside it.

Finding the Area of Quadrilaterals circumscribing a circle.

---

Formulas: Radius of Inscribed and Circumscribed Circle in a Triangle

One of the common word problems in plane geometry is finding either the radius of the inscribed circle or the radius of circumscribed circle in a triangle. Familiarize yourself with the different formulas of finding the radius according to the kind of triangles involved. The efficiency of getting the correct solutions for every problems is directly proportional to number of times you practice solving similar problems.

Right Triangle: Inscribed and Circumscribed Circle Formulas

Isosceles Triangle: Inscribed and Circumscribed Circle Formulas

Equilateral Triangle: Inscribed and Circumscribed Circle Formulas

Scalene Triangle: Inscribed and Circumscribed Circle Formulas

---

Derivation of Formula for the Radius of Circumcircle

Most of the Plane Geometry problems in triangle could be easy solve by direct substitution using the applicable formula according to the given value of the problems. To find the radius of the circumscribed circle (circumcircle) given the value of the area and the three sides, simply divide the product of the three sides by 4 times the area of the triangle. In other words, the radius of the circumcircle is the ratio of the product of the three sides to 4 times the area.

If you are wondering how we came up with the formula, just follow the derivation below.

• If are looking for the radius of incircle see the derivation of formula for radius of incircle.

The Formula

where R = radius of Circumscribed Circle and a, b and c are the sides.

Derivation of the radius of Circumcircle

Finally,

where R = radius of Circumscribed Circle and a, b and c are the sides.

---

Derivation of Formula for the Radius of Incircle

Most of the Plane Geometry problems in triangle could be easy solve by direct substitution using the applicable formula according to the given value of the problems. To find the radius of the inscribed circle (incircle) given the value of the area and the three sides, simply divide the area by the half of the perimeter (s). In other words, the radius of the incircle is the ratio of the Area of the triangle to its half of the Perimeter.

If you are wondering how we came up with the formula, just follow the derivation below.

• If are looking for the radius of circumcircle see the derivation of formula for radius of circumcircle.

The Formula

where A = area of the triangle and s = ½ (a + b + c).

Derivation of the radius of Incircle

Finally,

where A = area of the triangle and s = ½ (a + b + c).

---

Special Centers in a Triangle

Centroid

Centroid is the point of intersection of all the medians of a triangle. It is the geometric of a plane figure.

Incenter

Incenter is the point of intersection of all angle bisectors in a triangle. It is also the center of the inscribed circle (incircle) in a triangle.

where A = area of the triangle and s = ½ (a + b + c).

• See the derivation of formula for radius of incircle.

Circumcenter

Circumcenter is the point of intersection of all perpendicular bisectors of a triangle. It is also the center of the circumscribed circle (circumcircle).

where R = radius of Circumscribed Circle and a, b and c are the sides.

Orthocenter

Orthocenter is the point of intersection of all the altitudes of a triangle. Like circumcenter, it can be inside or outside the triangle.

Excenter

Excenter is the center of the escribed circle.

TRIVIA

A line that passes through the incenter and orthocenter of a triangle is called Euler's line.

---

Special Lines in a Triangle

Side

Side of a triangle is a line segment that connects two vertices. Triangle has three sides.

Vertex

Vertex is the point of intersection of two sides of triangle.

Median, m

A median of a triangle is a segment from vertex to the midpoint of the opposite side. A triangle has three medians, and these three will intersect at the centroid.

Length of Median: (Apollonius)

Properties

Some fascinating properties of the medians of a triangle:

1. The fact that the three medians always meet at a single point is interesting in its own right.
2. Each median divides the triangle into two smaller triangles which have the same area.
3. The centroid (point where they meet) is the center of gravity of the triangle.
4. The three medians divide the triangle into 6 smaller triangles that all have the same area, even though they may have different shapes.

Angle Bisector

An Angle Bisector of a triangle is a segment or ray that bisects an angle and extends to the opposite side. It is drawn from vertex to the opposite side of the triangle. Since there are three included angles of the triangle, there are also three angle bisectors, and these three will intersect at the incenter.

Length of Angle Bisector:

Altitude, h

An altitude of a triangle is a segment from a vertex perpendicular to the opposite side. The altitudes of the triangle will intersect at a common point called orthocenter.

Length of Altitude:

Midsegment

Midsegment of a Triangle is a line segment joining the midpoints of two sides of a triangle. A triangle has 3 possible midsegments.

Properties

1. The midsegment is always parallel to the third side of the triangle. In the figure above, drag any point around and convince yourself that this is always true.
2. The midsegment is always half the length of the third side. In the figure above, drag point A around. Notice the midsegment length never changes because the side BC never changes.
3. A triangle has three possible midsegments, depending on which pair of sides is initially joined.

Perpendicular Bisector

Perpendicular bisector of the triangle is a perpendicular line that crosses through midpoint of the side of the triangle. The three perpendicular bisectors are worth noting for it intersects at the center of the circumscribing circle of the triangle. The point of intersection is called the circumcenter.

---

Mensuration Formulas of the Triangles

Definition of a Triangle

Triangle is a polygon with three sides and three vertices. It can also be defined as closed figure bounded by three straight lines called sides. If three sides of a triangle are equal, it is an equilateral triangle. An equilateral triangle is also equiangular. It two sides are equal, it is an isosceles triangle. While, scalene triangle is a triangle with no two sides are equal.

In Euclidean geometry any three points, when non-collinear, determine a unique triangle and a unique plane (i.e. a two-dimensional Euclidean space). Egyptian triangle is a right triangle with sides equivalent to 3, 4 and 5 units.

Measures of Angles

A degree (°) is defined as the measure of the central angle subtended by an arc of a circle equal to 1/360 of circumference of the circle. A minute (') is equal to 1/60 of a degree. A second ('') is equal to 1/60 of a minute.

A radian (rad) is defined as the measure of the central angle subtended by an arc of a circle equal to the radius of the circle.

The circumference of a circle is defined as the length of the total arc of the circle, is numerically equal to 2π times the radius and subtends an angle of 360°

TIPS:

1. Complementary angles are two angles whose sum is 90° or right angle.

2. Supplementary angles are two angles whose sum is 180° or straight angle.

3. Explementary angles are two angles whose sum is 360° or perigon.

In general, there are only two kinds of triangle:

1. Right triangle - a triangle with one interior angle is exactly 90°.

2. Oblique triangle - a triangle without a right angle.

Oblique triangle may either be:

1. Acute triangle - a triangle with all of interior angles are less than 90°.

2. Oblique triangle - a triangle with one of the interior angles is greater than 90°.

The follwing give the basic formulas using different kinds of triangles:

RIGHT TRIANGLES

ISOSCELES RIGHT TRIANGLES

30° - 60° TRIANGLES

EQUILATERAL TRIANGLE

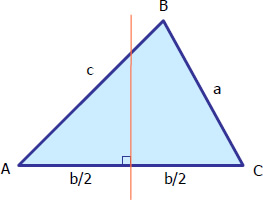
OBLIQUE TRIANGLE (given three sides)

Other Formulas of a Triangle:

• Given two sides and included angle
• Given three angles and one side
• Triangle with inscribed circle
• Triangle inscribed in a circle
• Triangle with escribed circle

Symbols and Notations

a, b, c = lengths of sides of a triangle

A = area of a figure or polygon

V = volume of a solid

C = circumference of a circle

P = perimeter

h_c = altitude to side c

d = diagonal of a polygon or diameter of a circle

r = radius of a circle, or a radius of an inscribed circle in a polygon (apothem)

R = radius of circumscribed circle

s = side of a polygon, or one-half of the perimeter of a triangle, or length of a circular arc.

TRIVIA:

The symbols + and - for plus and minus, respectively was introduced by German mathematician and astronomer, Johannes Regiomontanus in 1456.

Introduction to Plane Geometry

The term "geometry" was derived from the Greek works, "ge" meaning earth and "metria" meaning measurement. Euclid (330–283275 BC), sometimes called Euclid of Alexandria to distinguish him from Euclid of Megara, was a Greek mathematician, often referred to as the "Father of Geometry". His book "Elements" is one of the most influential works in the history of mathematics, serving as the main textbook for teaching mathematics (especially geometry. The book give more emphasis on Plane Geometry which concerns with geometric figures constructed on a plane surface or geometrical shape of two dimensions (for example angle, triangle, conic sections, etc.).

Archimedes (287-212 BC) considered the greatest mathematician of antiquity and one of the greatest of all time Archimedes anticipated modern calculus and analysis by applying concepts of infinitesimals and the method of exhaustion to derive and rigorously prove a range of geometrical theorems, including the area of a circle, the surface area and volume of a sphere, and the area under a parabola. He contributed so much to Solid geometry which concerns with three dimensional geometric figures such as cylinder, sphere, pyramid, angle between planes.

Claudius Ptolemy (AD 90 – c. 168) deals with the application of geometry to astronomy.

Solid Mensuration

Solid Mensuration is the study of various solids. It treats mainly with the surfaces areas, volumes of different solids, height, length, and other relations between geometric figures. It is probably the most extensively used in the practice of engineering. The concept and knowledge about this subject is a much needed for an engineer to become successful in any project construction.

Study of Plane Geometry

The study of Plane geometry sets the fundamental for the study of Solid or Space Geometry. Make sure to gain knowledge and always have time to practice solved problems, that is the most excellent way to make your dream come true - be an engineer someday.

Topic